Compound interest online test - Aptitude
Welcome to freeonlinetest online exam portal, here you will get 2000+ Compound Interest With formulae. As you know Aptitude is one of the important topics for competitive exams like Banking, SSC CGL, SSC MTS, SSC Group D, Railway Group D, Police Constable Exams, etc.
Compound Interest is also part of Quantitative Aptitude. Here you will get expected questions prepared by experts which could help in your exam in the aptitude section.
Compound Interest - Basic Formulas, Shortcuts, Rules, Tricks & Tips
If A = Amount, P = Principal, r = Rate of Compound Interest (C.I.), n = no. of years then,
A = P$(1 + r/100)^n$,
C.I. = A - P
C.I. = P$[(1 + r/100)^n - 1]$
When interest compounded annually : A= P$(1 + r/100)^n$
When interest compounded half yearly : A= P$(1 + {r/2}/100)^{2n}$
When interest compounded quarterly : A= P$(1 + {r/4}/100)^{4n}$
When interest compounded monthly: A= P$(1 + {r/12}/100)^{12n}$
If there are distinct rates of interest for distinct time periods i.e.,
Rate for 1st year → $r_1$%
Rate for 2nd year → $r_2$%
Rate for 3rd year → $r_3$% and so on
Then, A = P$(1 + r_1/100)(1 + r_2/100)(1 + r_3/100)$...
C.I. = A – P
If the time is in fractional form i.e.,t = nF, then
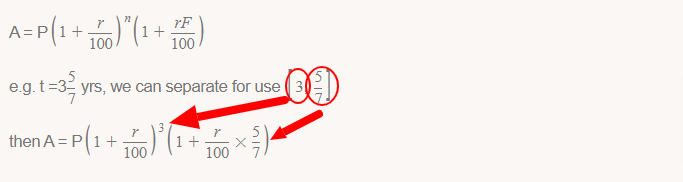
The difference between C.I. and S.I. on a sum 'P' in 2 years at the rate of R% rate of compound interest will be
C.I – S.I. = P$(R/100)^2 = {S.I. × R}/200$
For 3 years, C.I. – S.I. = P$(R/100)^2 × (3 + R/100)$
If a sum becomes 'n' times of itself in 't' years on compound interest, then
R% = $[n^{1/t} - 1] × 100%$
The simple interest for a certain sum for 2 years at an annual rate interest r% is S.I., then
C.I. = S.I.$(1 + r/200)$
A certain sum at C.I. becomes x times in $t_1$ year and y times in $t_2$ years then
$x^{1/t_1} = y^{1/t_2}$
 |
Online Test - 1 (Compound Interest) TAKE TEST
Number of questions : 20 | Time : 30 minutes |
 |
Online Test - 2 (Compound Interest) TAKE TEST
Number of questions : 20 | Time : 30 minutes |
 |
Online Test - 3 (Compound Interest) TAKE TEST
Number of questions : 20 | Time : 30 minutes |
 |
Online Test - 4 (Compound Interest) TAKE TEST
Number of questions : 20 | Time : 30 minutes |
 |
Online Test - 5 (Compound Interest) TAKE TEST
Number of questions : 20 | Time : 30 minutes |
Compound Interest:
We have provided useful formulae and hints for the Compound Interest category. Requesting you to refer below points before taking any CI test.
While calculating compound interest, the simple interest which is calculated for the principal of first year will add to the principal which we taken already. The addition of this amount will be the principle for the next year. For this amount simple is calculated for second year and added to principal for second year. It will go on increase like this. Finally principal is subtracted from last year amount. The result of this subtraction gives compound interest. It is denoted by CI.
Previous year solved Questions:
1. What total amount will Ravali get in 2 yr. if she invests Rs. 5000 to obtain compound interest at the rate of 5 pcpa?
A) Rs. 5511.50
B) Rs. 5312.50
C) Rs. 5542.50
D) Rs. 5512.50
E) None of these
Ans: D
Solution: Given data P = 5000, R = 5%, n = 2yr.
Formulae: Amount = P $( 1 + R/100)^ n$
=> 5000 $ ( 1 + 5/100) ^2$
=>5000 x $(21/20)^2$
=> Rs.5512.50
2. The population of a city is 126800. It increases by 15% in the first year and decreases by 20% in the second year. What is the population of the town at the end of 2 yr?
A) 174984
B) 135996
C) 116656
D) 145820
E) None of these
Ans: C
Population after 2 yrs.
P $ { ( 1 + {R_1}/100)} × {( 1 – {R_2}/100)}$
=> 126800 ${( 1+ 15/100)}× {( 1 – 20/100)}$
=> 126800 $ (1+ 3/20) × (1 – 1/5) $
= > 116656

